Trigonometría
La trigonometría es el estudio de las funciones seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.
Las funciones trigonométricas
La trigonometría como rama de las matemáticas realiza su estudio en la relación entre los lados y ángulos de un triángulo rectángulo, con una aplicación inmediata en geometría y sus aplicaciones. Para el desarrollo de este fin se definieron una serie de funciones que han sobrepasado su fin original, convirtiéndose en elementos matemáticos estudiados en sí mismos y con aplicaciones en los campos más diversos.
Razones trigonométricas
- El seno (abreviado como sen, o sin por llamarse "senos" en latín) es la razón entre el cateto opuesto sobre la hipotenusa,
-
-

-
- El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa,
-
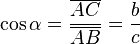
- La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente,
-

-
Valor de las funciones trigonométricas
A continuación algunos valores de las funciones que es conveniente recordar:
 |  |
| Circunferencia en radianes. | Circunferencia en grados sexagesimales. | |
-
-
| Radianes | Grados sexag. | seno | coseno | tangente | cosecante | secante | cotangente |
|---|
 |  |  |  |  |  | 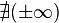 |  | 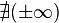 |
 |  | 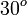 |  |  | 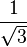 | 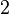 | 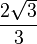 |  |
 |  |  |  |  |  |  |  |  |
 | 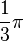 | 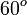 |  |  |  | 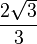 | 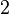 | 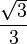 |
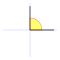 |  |  |  |  | 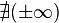 |  | 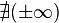 |  |
Para el cálculo del valor de las funciones trigonométricas se confeccionaron tablas trigonométricas. La primera de estas tablas fue desarrollada por Johann Müller Regiomontano en 1467, que nos permiten, conocido un ángulo, calcular los valores de sus funciones trigonométricas. En la actualidad dado el desarrollo de la informática, en prácticamente todos los lenguajes de programación existen librerías de funciones que realizan estos cálculos, incorporadas incluso en calculadoras electrónicas de bolsillo, por lo que el empleo actual de las tablas resulta obsoleto.
Sentido de las funciones trigonométricas
Dados los ejes de coordenadas cartesianas xy, de centro O, y una circunferencia goniométrica (circunferencia de radio la unidad) con centro en O; el punto de corte de la circunferencia con el lado positivo de las x, lo señalamos como punto E.
Nótese que el punto A es el vértice del triángulo, y O es el centro de coordenada del sistema de referencia:
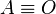
a todos los efectos.
La recta r, que pasa por O y forma un ángulo  sobre el eje de las x, corta a la circunferencia en el punto B, la vertical que pasa por B, corta al eje x en C, la vertical que pasa por E corta a la recta r en el punto D.
sobre el eje de las x, corta a la circunferencia en el punto B, la vertical que pasa por B, corta al eje x en C, la vertical que pasa por E corta a la recta r en el punto D. Por semejanza de triángulos:
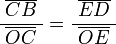
Los puntos E y B están en la circunferencia de centro O, por eso la distancia  y
y  son el radio de la circunferencia, en este caso al ser una circunferencia de radio = 1, y dadas las definiciones de las funciones trigonométricas:
son el radio de la circunferencia, en este caso al ser una circunferencia de radio = 1, y dadas las definiciones de las funciones trigonométricas: 


tenemos:

La tangente es la relación del seno entre el coseno, según la definición ya expuesta.
Primer cuadrante
Para ver la evolución de las funciones trigonométricas según aumenta el ángulo, daremos una vuelta completa a la circunferencia, viéndolo por cuadrantes, los segmentos correspondientes a cada función trigonométrica variaran de longitud, siendo esta variación función del ángulo, partiendo en el primer cuadrante de un ángulo cero.
Partiendo de esta representación geométrica de las funciones trigonométricas, podemos ver las variaciones de las funciones a medida que aumenta el ángulo  .
. Para 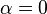 , tenemos que B, D, y C coinciden en E, por tanto:
, tenemos que B, D, y C coinciden en E, por tanto: 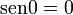

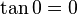
Si aumentamos progresivamente el valor de  , las distancias
, las distancias  y
y 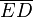 aumentarán progresivamente, mientras que
aumentarán progresivamente, mientras que  disminuirá.
disminuirá. Percatarse que el punto B es de la circunferencia y cuando el ángulo aumenta se desplaza sobre ella.
El punto E es la intersección de la circunferencia con el eje x y no varia de posición.
Los segmentos:  y
y  están limitados por la circunferencia y por tanto su máximo valor absoluto será 1, pero
están limitados por la circunferencia y por tanto su máximo valor absoluto será 1, pero 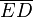 no está limitado, dado que D es el punto de corte de la recta r que pasa por O, y la vertical que pasa por E, en el momento en el que el ángulo
no está limitado, dado que D es el punto de corte de la recta r que pasa por O, y la vertical que pasa por E, en el momento en el que el ángulo  rad, la recta r será la vertical que pasa por O. Dos rectas verticales no se cortan, o lo que es lo mismo la distancia
rad, la recta r será la vertical que pasa por O. Dos rectas verticales no se cortan, o lo que es lo mismo la distancia 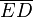 será infinita.
será infinita. El punto C coincide con A y el coseno vale cero. El punto B esta en el eje y en el punto más alto de la circunferencia y el seno toma su mayor valor: uno.
Para un ángulo recto las funciones toman los valores:


-

Segundo cuadrante
Cuando el ángulo  supera el ángulo recto, el valor del seno empieza a disminuir según el segmento
supera el ángulo recto, el valor del seno empieza a disminuir según el segmento  , el coseno aumenta según el segmento
, el coseno aumenta según el segmento  , pero en el sentido negativo de las x, el valor del coseno toma sentido negativo, si bien su valor absoluto aumenta cuando el ángulo sigue creciendo.
, pero en el sentido negativo de las x, el valor del coseno toma sentido negativo, si bien su valor absoluto aumenta cuando el ángulo sigue creciendo. La tangente para un ángulo  inferior a
inferior a  rad se hace infinita en el sentido positivo de las y, para el ángulo recto la recta vertical r que pasa por O y la vertical que pasa por E no se cortan, por lo tanto la tangente no toma ningún valor real, cuando el ángulo supera los
rad se hace infinita en el sentido positivo de las y, para el ángulo recto la recta vertical r que pasa por O y la vertical que pasa por E no se cortan, por lo tanto la tangente no toma ningún valor real, cuando el ángulo supera los  rad y pasa al segundo cuadrante la prolongación de r corta a la vertical que pasa por E en el punto D real, en el lado negativo de las y, la tangente
rad y pasa al segundo cuadrante la prolongación de r corta a la vertical que pasa por E en el punto D real, en el lado negativo de las y, la tangente 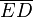 por tanto toma valor negativo en el sentido de las y, y su valor absoluto disminuye a medida que el ángulo
por tanto toma valor negativo en el sentido de las y, y su valor absoluto disminuye a medida que el ángulo 
 rad. aumenta progresivamente hasta los
rad. aumenta progresivamente hasta los Resumiendo: en el segundo cuadrante el seno de  ,
,  , disminuye progresivamente su valor desde 1, que toma para
, disminuye progresivamente su valor desde 1, que toma para  rad, hasta que valga 0, para
rad, hasta que valga 0, para  rad, el coseno,
rad, el coseno, , toma valor negativo y su valor varia desde 0 para
, toma valor negativo y su valor varia desde 0 para  rad, hasta –1, para
rad, hasta –1, para  rad.
rad. La tangente conserva la relación:

incluyendo el signo de estos valores.
Para un ángulo llano tenemos que el punto D esta en E, y B y C coinciden en el eje de las xE, con lo que tenemos: en el lado opuesto de



Tercer cuadrante
En el tercer cuadrante, comprendido entre los valores del ángulo  rad a
rad a  rad, se produce un cambio de los valores del seno el coseno y la tangente, desde los que toman para
rad, se produce un cambio de los valores del seno el coseno y la tangente, desde los que toman para  rad:
rad: 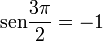


Cuando el ángulo  aumenta progresivamente, el seno aumenta en valor absoluto en el sentido negativo de las y, el coseno disminuye en valor absoluto en el lado negativo de las x, y la tangente aumenta del mismo modo que lo hacia en el primer cuadrante.
aumenta progresivamente, el seno aumenta en valor absoluto en el sentido negativo de las y, el coseno disminuye en valor absoluto en el lado negativo de las x, y la tangente aumenta del mismo modo que lo hacia en el primer cuadrante. A medida que el ángulo crece el punto C se acerca a O, y el segmento  , el coseno, se hace más pequeño en el lado negativo de las x.
, el coseno, se hace más pequeño en el lado negativo de las x. El punto B, intersección de la circunferencia y la vertical que pasa por C, se aleja del eje de las x, en el sentido negativo de las y, el seno,  .
. Y el punto D, intersección de la prolongación de la recta r y la vertical que pasa por E, se aleja del eje las x en el sentido positivo de las y, con lo que la tangente, 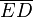 , aumenta igual que en el primer cuadrante
, aumenta igual que en el primer cuadrante Cuando el ángulo  alcance
alcance  rad, el punto C coincide con O y el coseno valdrá cero, el segmento
rad, el punto C coincide con O y el coseno valdrá cero, el segmento  será igual al radio de la circunferencia, en el lado negativo de las y, y el seno valdrá –1, la recta r del ángulo y la vertical que pasa por E serán paralelas y la tangente tomara valor infinito por el lado positivo de las y.
será igual al radio de la circunferencia, en el lado negativo de las y, y el seno valdrá –1, la recta r del ángulo y la vertical que pasa por E serán paralelas y la tangente tomara valor infinito por el lado positivo de las y. El seno el coseno y la tangente siguen conservando la misma relación:

que se cumple tanto en valor como en signo, nótese que cuando el coseno vale cero, la tangente se hace infinito.
Cuarto cuadrante
En el cuarto cuadrante, que comprende los valores del ángulo  entre
entre  rad y
rad y  rad, las variables trigonométricas varían desde los valores que toman para
rad, las variables trigonométricas varían desde los valores que toman para  rad:
rad: 


hasta los que toman para  rad pasando al primer cuadrante, completando una rotación:
rad pasando al primer cuadrante, completando una rotación: 

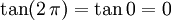
como puede verse a medida que el ángulo  aumenta, aumenta el coseno
aumenta, aumenta el coseno  en el lado positivo de las x, el seno
en el lado positivo de las x, el seno  disminuye en el lado negativo de las y, y la tangente
disminuye en el lado negativo de las y, y la tangente 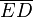 y. también disminuye en el lado negativo de las
y. también disminuye en el lado negativo de las Cuando  , vale
, vale  ó
ó  al completar una rotación completa los puntos B, C y D, coinciden en E, haciendo que el seno y la tangente valga cero, y el coseno uno, del mismo modo que al comenzarse el primer cuadrante.
al completar una rotación completa los puntos B, C y D, coinciden en E, haciendo que el seno y la tangente valga cero, y el coseno uno, del mismo modo que al comenzarse el primer cuadrante. Dado el carácter rotativo de las funciones trigonométricas, se puede afirmar en todos los casos:



Que cualquier función trigonométrica toma el mismo valor si se incrementa el ángulo un número entero de rotaciones completas.
Seno y coseno, funciones complejas
El seno y coseno se definen en matemática compleja, gracias a la fórmula de Euler como:


Por lo tanto, la tangente quedará definida como:
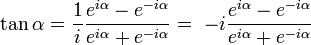
Siendo 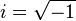 (también puede representarse como j).
(también puede representarse como j). Es preciso destacar, que todas las formulas trigonometricas anteriores, son derivadas del Teorema de Pitágoras.

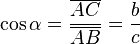









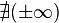



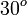


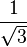
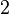
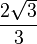







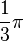
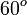
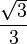



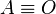
 sobre el eje de las x, corta a la circunferencia en el punto B, la vertical que pasa por B, corta al eje x en C, la vertical que pasa por E corta a la recta r en el punto D.
sobre el eje de las x, corta a la circunferencia en el punto B, la vertical que pasa por B, corta al eje x en C, la vertical que pasa por E corta a la recta r en el punto D.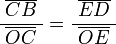
 y
y  son el radio de la circunferencia, en este caso al ser una circunferencia de radio = 1, y dadas las definiciones de las funciones trigonométricas:
son el radio de la circunferencia, en este caso al ser una circunferencia de radio = 1, y dadas las definiciones de las funciones trigonométricas:



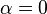 , tenemos que B, D, y C coinciden en E, por tanto:
, tenemos que B, D, y C coinciden en E, por tanto: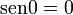

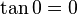
 y
y 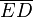 aumentarán progresivamente, mientras que
aumentarán progresivamente, mientras que  disminuirá.
disminuirá. rad, la recta r será la vertical que pasa por O. Dos rectas verticales no se cortan, o lo que es lo mismo la distancia
rad, la recta r será la vertical que pasa por O. Dos rectas verticales no se cortan, o lo que es lo mismo la distancia 


 rad se hace infinita en el sentido positivo de las y, para el ángulo recto la recta vertical r que pasa por O y la vertical que pasa por E no se cortan, por lo tanto la tangente no toma ningún valor real, cuando el ángulo supera los
rad se hace infinita en el sentido positivo de las y, para el ángulo recto la recta vertical r que pasa por O y la vertical que pasa por E no se cortan, por lo tanto la tangente no toma ningún valor real, cuando el ángulo supera los  rad. aumenta progresivamente hasta los
rad. aumenta progresivamente hasta los  rad, el coseno,
rad, el coseno,



 rad, se produce un cambio de los valores del seno el coseno y la tangente, desde los que toman para
rad, se produce un cambio de los valores del seno el coseno y la tangente, desde los que toman para 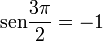


 rad, el punto C coincide con O y el coseno valdrá cero, el segmento
rad, el punto C coincide con O y el coseno valdrá cero, el segmento  rad, las variables trigonométricas varían desde los valores que toman para
rad, las variables trigonométricas varían desde los valores que toman para 




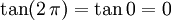
 al completar una rotación completa los puntos B, C y D, coinciden en E, haciendo que el seno y la tangente valga cero, y el coseno uno, del mismo modo que al comenzarse el primer cuadrante.
al completar una rotación completa los puntos B, C y D, coinciden en E, haciendo que el seno y la tangente valga cero, y el coseno uno, del mismo modo que al comenzarse el primer cuadrante.




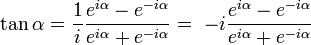
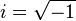 (también puede representarse como j).
(también puede representarse como j).